2021. 4. 4. 20:49ㆍComputer(인강)/네트워크
안녕하세요 bannavi입니다^ㅅ^
오늘은 동적 라우팅의 개요에 대해서 배워볼거에요
바로 시작하겠습니다

라우팅 프로토콜
개요 : 라우팅 프로토콜은 정적(Static) & 동적(Dynamic)으로 구분된다
정적 라우팅 : 경로 정보를 라우터에 미리 저장하여 패킷 전송
동적 라우팅 : 경로 정보가 네트워크 상황에 따라 더 빠른 경로로 변경되어 패킷 전송
아래 그림의 AS는 라우터 집단이라고 보시면 됩니다
EGP의 가장 대표적인 프로토콜로 BGP가 있습니다.
IGP의 대표적인 프로토콜로 RIP, OPSF

라우팅 알고리즘
역할 : 목적지까지의 최적 경로를 계산하고 라우팅 테이블에 업데이트
1. 동적으로 라우팅 테이블을 유지 및 관리하는 알고리즘
2. Distance Vector & Link State routing으로 구분한다
Distance Vector
분산 업데이트, 각 라우터들에 의해 최소 비용 경로 계산 -> 인접 노드와 교환
소규모 네트워크, 주기적이며 비동기 방식
Link State
중앙 집중형 업데이트, 네트워크 전체 정보를 통해서 최소 비용 경로 계산
대규모 네트워크에 적합, 이벤트 기반의 라우팅 테이블 관리
Distance Vector 라우팅
거리 + 방향
목적지 IP까지의 거리 = Hop 카운트 = 라우터와 라우터 사이의 거리 + 인터페이스 방향
인접 라우터들과 주기적으로 라우팅 테이블을 교환하여 확인 및 관리
인접 라우팅 테이블만 관리 -> 메모리 절약
비교적 구성이 간단
주기적 라우팅 테이블 업데이트 -> 무의미한 트래픽 발생 가능
Convergence time(라우팅 테이블 업데이트 시간)이 느리다
소규모 네트워크에 적용
1969년 Bellman-Ford 알고리즘에 기반하여 설계, APANET 최초의 라우팅 알고리즘으로 고안
Bellman-Ford 알고리즘
최단 경로 문제를 풀어주는 알고리즘
예시)
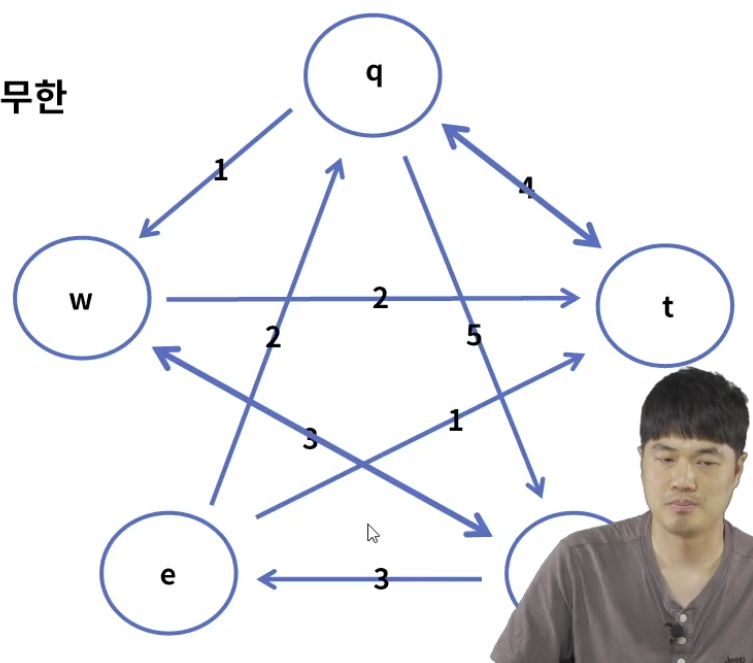
노드 : 5개(q,w,e,r,t), 간선 : 10개(양방향 포함)
최단 경로 : dq(e) = q에서 e까지 총 경로 (dq(e)의 d는 distance를 의미합니다)
비용 : c(q,w) = 인접 노드간의 비용 (c는 cost의 약자이구요. 즉, q와 w사이의 cost는 얼마? 의 의미입니다)
기존에 가지고 있는 cost보다 더 적은값이 있으면 그걸 선택하는것이 우선이기 때문에,
이러한식으로 distance q에서 e까지는 min(가장작은수)를 택해라.
그래서 아래의 집합 중에서 가장 작은 경우의 수를 선택하는것을 아래와 같이 수식으로 나타낼 수 있습니다
각각의 경로별로 값을 구해서 가장 작은 값을 구하는게 갱신되어지는 라우팅 업데이트가 되는 부분이라고 볼 수 있습니다
갱신 : dq(e) = min {
c(q,w) + dw(e)
c(q,r) + dr(e)
c(q,t) + dt(e)
}

위의 내용을 직접 풀어보는 시간을 가져볼게요
Bellman-Ford 알고리즘 - 상세
최단 경로 : dq(e)
비용 : c(q,w) = 1, c(q,r) = 5, c(q,t) = 4
q에서 e까지 직접 연결되어있는 링크는 없습니다
최소값 : dq(e) = min {
1 + dw(e)
5 + dr(e)
4 + dt(e)
}

dw(e) = c(w,t) + c(t,e) = 2 + 1 = 3
dr(e) = c(r,e) = 3
dt(e) = c(t,e) = 1
그리고 이걸 더하면 최적 경로가 나오게 됩니다

dq(e) = min { 4, 8, 5 } = 4
이러한 알고리즘은 주기적으로 업데이트를 하게 되어있습니다
주기적 업데이트
- 연결 링크의 비용 변경
- 최단 거리의 변경
이러한 알고리즘은 아래와 같은 일련의 과정을 거쳐가고요.
Listening -> Change -> Estimate -> Notify -> Update
친절하게 한글로 표현 해보면 아래와 같습니다
기다림 -> 최단 거리 값 & 연결 링크 비용 변경 -> 인접 노드로 전달
위와 같은 내용이 Bellman Ford 알고리즘의 내용이라고 볼 수 있습니다.
Bellman-Ford 알고리즘 상세
이러한 알고리즘은 테이블로 구성이 되어있는데요.
그래서 이것을 각 노드의 인접 경로들로 하나의 테이블을 짜서 이렇게 보통 표시를 합니다
각 노드의 인접 경로 별 Cost

알고리즘을 처음에 구상했을때 위와같이 그림을 그린뒤 아래와 같이 테이블을 만들고
수도코드를 작성해서 C언어, java로 알고리즘을 짜는거죠.
q에서 q로 가는거는 당연히 자기 자신이기 때문에 0이겠죠? 그래서 우하향 대각선은 모두 0이에요.
q에서 e로 가는건 없으니 비워져 있는것이고요


그리고 난 다음, 업데이트가 이루어져야 되겠죠?
t가 q에게 e까지의 경로 비용을 전달, q는 e까지의 경로 계산하여 업데이트해주게 됌

그 다음, t가 없데이트를 한번 더 합니다

t가 w에게 e까지의 경로 비용을 전달, w는 e까지의 경로 계산하여 업데이트

그리고 나서, t가 다시 w에게 q까지의 경로 비용을 전달, w는 q까지의 경로 계산하여 업데이트


w가 q에게 e까지의 경로 비용을 전달, q는 e까지의 경로 계산하여 업데이트

더 짧은 경로가, 최적의 경로가 발생을 하였으니 수정을 해줘야겠죠

이렇게 쫌쫌따리 무수한 과정들을 거치고 나면...!
모든 라우팅 테이블이 업데이트 완료 -> 컨버전스 타임 with Change -> 업데이트
그럼 이렇게 모든 테이블에 값이 표시가 되게 됩니다.

Link State 라우팅
1. 링크 상태를 보겠다는것
2. 즉, 회선의 대역폭을 고려하여 가중치를 부여
3. 네트워크 토폴로지 경로를 모든 라우터들에게 전달
4. 라우팅 정보가 변경되는 이벤트 건에 대해서만 전파 -> 네트워크 트래픽 감소
5. 전체 네트워크상의 라우터들의 테이블 정보가 동일하게 유지
6. 각 라우터들은 최상의 경로를 계산 -> Dijkstra's algorithm
7. 1959년 컴퓨터 과학자 Dijkstra(1972년 튜링상 수상)가 발표
8. 1980년 ARPANET에서 개발 -> 1989년 OSPF 발표
Dijkstra's 알고리즘
주어진 출발지와 목적지 사이의 최단 경로 문제를 푸는 알고리즘
예시)
노드 5개, 간선 : 10개(양방향 포함), 초기값은 무한
출발지는 q -> 목적지는 e
이런식으로 우선 네트워크 토폴리지를 구성합니다

이런 수식을 알아보면, 첫번째 S는 공집합이죠.
현재 네트워크 토폴리지 노드에서 아무도 업데이트를 하지 않은 상태에요.
S = {}
그리고 distance q에요. q에서 q로 가는거는 당연히 0이겠죠
d[q] = 0
아직까지 하나도 업데이트가 이뤄지지 않은 상태
d[w] = 무한
d[e] = 무한
d[r] = 무한
d[t] = 무한
Q = { q, w, e, r, t }
q에서 e까지 가는 경로의 수를 한번 봅시다
q -> e
그럼 이제 q가 발동을 하는거죠.
S = {q}
그럼 이제 q가 붙어있는 w, r, t를 업데이트 하게 됩니다

d[q] = 0
d[w] = 1
(q에서 e까지 가는 경로는 없으므로 무한이 됩니다)
d[e] = 무한
d[r] = 5
d[t] = 4
Q = { w, e, r, t }
그 다음은 w를 집어넣고요
S = { q, w }
업데이트를 해야되겠죠?
d[q] = 0
d[w] = 1
d[e] = 무한
d[r] = 5 -> 1 + 3 = 4

기존에는 q에서 r까지 가려면 5가 걸렸는데
w경로를 이용해서 4가 됐네요
그럼 이제 5가 4로 대체가 되는거죠.
그리고 이후에 w가 t까지 가는것도 이후 업데이트 됩니다
d[t] = 4 -> 1 + 2 = 3
기존에는 q에서 t까지 가는 법이 4였는데
q를 거쳐 1 + 2해서 3이 되는거죠.

그럼 이런식으로 라우팅 테이블이 업데이트 되는 것입니다
나머지는 e, r, t가 남았다는것을 이렇게 표현하는거고요
Q = { e, r, t }
이번에는 r을 한번 업데이트 해볼게요
S = { q, w, r }
기존값은 그대로 가고요
d[q] = 0
d[w] = 1
r이 이제 e까지 가는 호스트를 q에게 전달하고요
q입장에서는 e까지 가는 경로가 없었어요

그러다가 q에서 r까지 가는 경로 5번과 e까지 가는 경로 3을 더하니 8이 됐어요
그런데 기존의 w와 r이 업데이트 되면서 이러한 경로가 생겨난거죠
1 + 3 + 3 = 7이네요.

그러면 기존에 8보다 더 빠른 경로가 발생했으니 7로 바뀌는것입니다(최적 경로)
d[e] = 무한 -> 5 + 3 = 8 -> 1 + 3 + 4 = 7
d[r] = 4
d[t] = 3
그리고 나머지는 e와 t가 남는거죠
Q = { e, t }
S = { q, w, r }이 업데이트를 하니 이 네트워크 토폴리지의 모든 경로가 다 나오게 된 것입니다
d[q] = 0
d[w] = 1
d[e] = 7
d[r] = 4
d[t] = 3
Q = { e, t }
결국에는 모든 값이 나오고 Q에 들어가 있는 이러한 가정들이 더해져서
이러한 네트워크 토폴로지가 완성이 되는 것입니다
Wrap up
1. 동적 라우팅은 네트워크 상황에 따라 경로 정보가 변경되어 패킷을 전송
2. Distance Vector 라우팅은 거리(hop count) + 방향이며 분산형으로 주기적으로 업데이트
3. Bellman-Ford 알고리즘을 사용하며 APANET 최초의 라우팅 알고리즘
4. Link State 라우팅은 회선의 대역폭을 고려하며 중앙 집중형으로 이벤트 기반으로 업데이트
5. Dijkstra's(다익스트라) 알고리즘을 사용하며 1980년 ARPANET에서 개발
'Computer(인강) > 네트워크' 카테고리의 다른 글
| 동적 라우팅 03. 동적 라우팅 - OSPF (0) | 2021.04.04 |
|---|---|
| 동적 라우팅 02. 동적 라우팅 BGP & RIP (0) | 2021.04.04 |
| IP주소와 라우팅 04. DHCP (0) | 2021.04.04 |
| IP주소와 라우팅 03. ICMP (0) | 2021.04.04 |
| IP주소와 라우팅 02. 라우터와 서브넷팅 (1) | 2021.04.04 |