부울대수와 논리식의 간편화 1
2021. 3. 19. 19:41ㆍComputer(인강)/컴퓨터 구조
728x90
반응형
안녕하세요 bannavi입니다^ㅅ^
오늘은~ 부울대수와 논리식의 간편화 첫번째 시간이에요
바로 시작해보도록 하겠습니다
부울 대수와 논리식의 간편화
1. 부울 대수(Boolean Algebra)
2. 논리식의 간편화 카노(Karnaugh)맵
2.9 부울 대수(Boolean Algebra)
참(True)와 거짓(False)을 판별할 수 있는 논리적 명제를 수학적 표현의 논리 전개 식으로 구현한것은
1854년 영국의 수학자 부울(G. Boole)에 의해서이다.
1. 논리 회로의 형태와 구조를 기술하는데 필요한 수학적인 이론
2. 부울 대수를 사용하면 변수들의 진리 표 관계를 대수식으로 표현하기에 용이
3. 동일한 성능을 갖는 더 간단한 회로를 만들기에 편리하다.
부울 대수의 기본 법칙
1. 교환법칙(commutative Law)
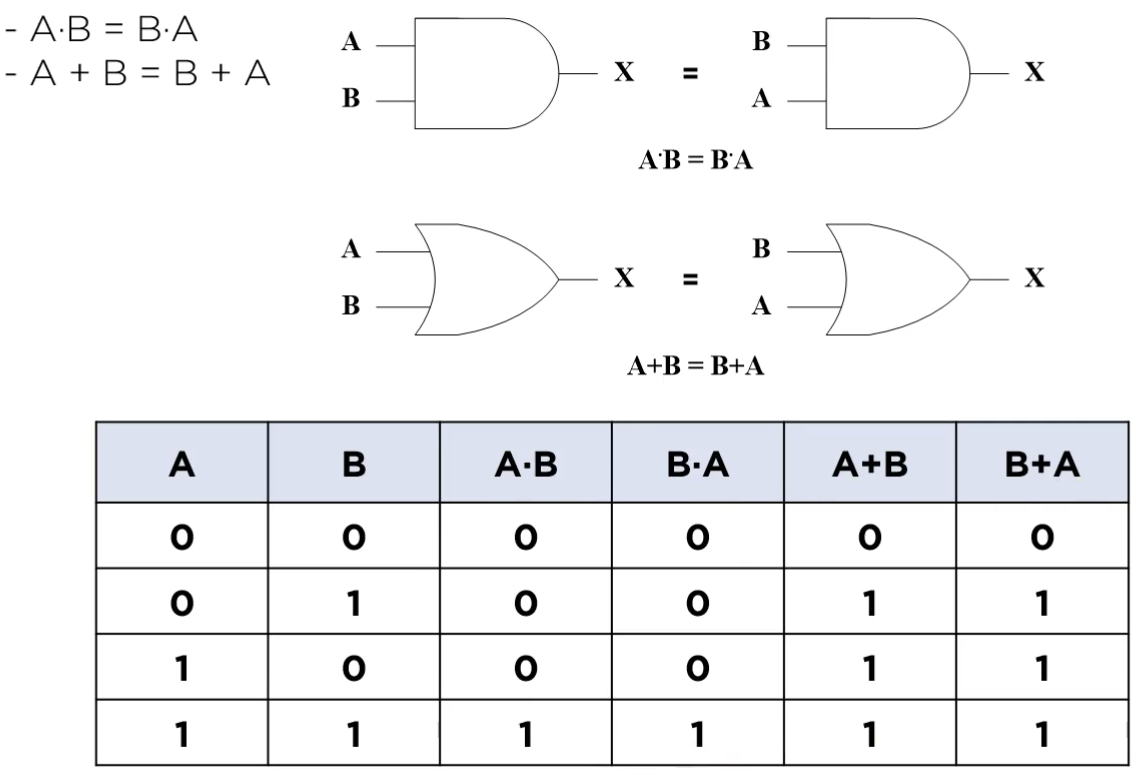
2. 결합법칙(Associative Law)

3. 분배법칙(Distributive Law)

4. 드모르강의 정리(De Morgan's theorm)

# 부울 대수를 이용한 간략화
* 다음 주어진 부울 식을 간략화 하시오
a가0이면 a가 1이기 때문에 a * a바는 0이다.(AND 연산)
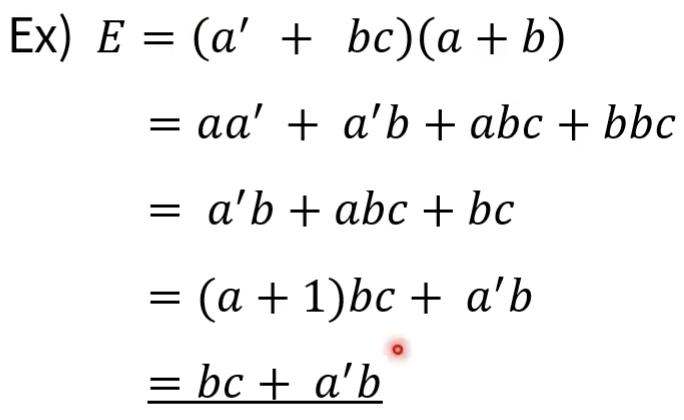
이런식으로 식이 간략하게 되면 기본적으로 부피가 줄어들 것입니다. 칩의 부피가 줄어든다..!
이런것이 우리가 부울 대수를 공부하는 이유입니다.
728x90
반응형
'Computer(인강) > 컴퓨터 구조' 카테고리의 다른 글
| 조합 & 기억 논리회로 1 (0) | 2021.03.19 |
|---|---|
| 부울대수와 논리식의 간편화 2 (0) | 2021.03.19 |
| 논리회로와 데이터 표현 2 (0) | 2021.03.19 |
| 논리회로와 데이터 표현 1 (0) | 2021.03.18 |
| 데이터의 종류 3 (0) | 2021.03.18 |